What of triangulations are we interested in?
Given a point configuration, there are several triangulations of the
convex hull of the points, using only the given points. For example,
the point configuration made by the vertices of a pentagon has five
triangulations indicated in the figure. 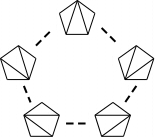 Triangulations are not merely existing, but they have some structure.
In the example of the pentagon, pairs of triangulations which
can change to each other by changing one edge (such operations are
called flips) are connected by dotted lines. So, with respect to this
local transformation, the five triangulations are forming a
structure of a pentagonal graph.
The aim of our research is to study the structure of triangulations in
general dimension.
Triangulations are not merely existing, but they have some structure.
In the example of the pentagon, pairs of triangulations which
can change to each other by changing one edge (such operations are
called flips) are connected by dotted lines. So, with respect to this
local transformation, the five triangulations are forming a
structure of a pentagonal graph.
The aim of our research is to study the structure of triangulations in
general dimension.
- Enumeration of triangulations
We have established algorithms to enumerate efficiently the
whole set of triangulations
for a given point set.
We also wrote programs implementing these algorithms.
Point configurations having triangulations of mathematical
interest often happen to be symmetric.
We also have devised an algorithm to enumerate regular
triangulations for such symmetric point configurations efficiently.
- Triangulations and dissections
In a triangulation, the components forming the division
are required to be touching nicely.
However, for some applications such as volume computation,
only the decomposition is enough, and they need not be touching
nicely (such decompositions are called
dissections).
We have found examples showing the difference of these
two classes of decomposition:
an example with the minimal dissection using less simplices
than minimal
triangulation, maximal dissection using more simplices than
maximal triangulation, upper and lower bounds for the size of
dissections.
- Incremental construction properties of simplicial complexes
Simplicial complexes are forming a superclass of triangulations.
Several kinds of incremental construction properties
of simplicial complexes have been known.
We have shown relations between some of these properties.
Study of such incremental construction properties are important
when handling geometric objects by computer.
Applications of triangulations
Polytopes often become easier to handle when divided into smaller
parts. There are many areas requiring techniques to handle three
dimensional point configurations, and triangulations become
important there.
Examples of such areas are computer graphics,
simulations for engineering, and handling 3D structures of DNA or proteins in
biology.
Back to home
 Last modified: Wed Jan 5 20:31:32 2005
Last modified: Wed Jan 5 20:31:32 2005
 Last modified: Wed Jan 5 20:31:32 2005
Last modified: Wed Jan 5 20:31:32 2005